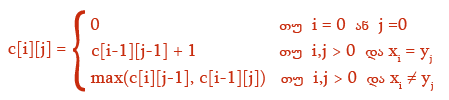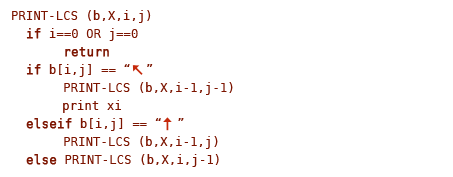წინა პოსტში მაგისტრატურის გამოცდა ვახსენე და დღეს მისთვის მოსამზადებლად მეორე ალგორითმს გავიხსენებ. ფსევდო კოდები და მაგალითები ისევ ”Introduction to Algorithms” წიგნიდან ავიღე 🙂
”უდიდესი საერთო ქვემიმდევრობის” (Longest Common Subsequence) პოვნა დინამიური პროგრამირების კიდევ ერთი კლასიკური ამოცანაა. ვთქვათ მოცემულია მიმდევრობები:
X = (A, B, C, B, D, A, B)
Y = (B, D, C, A, B, A)
ამ შემთხვევაში მათი ერთ-ერთი უდიდესი საერთო ქვემიმდევრობაა მიმდევრობა (B, C, B, A)
ცოტა უკეთ განვსაზღვროთ, თუ რა არის ქვემიმდევრობა:
ვთქვათ მოცემულია მიმდევრობა X = (x1, x2, … , xm).
Z = (z1, z2, …. , zk) არის მისი ქვევმიმდევრობა, თუ არსებობს (i1,i2..,ik) X-ის ინდექსების ისეთი მკაცრად ზრდადი მიმდევრობა, რომ ყველა j=1,2,… k მნიშვნელობისთვის სრულდებოდეს ტოლობა xij = zj.
არც ამ ამოცანის ამოსახსნელად გამოგვადგება ყველა ვარიანტის სრული გადარჩევა, რადგან ექსპონენციალურ დროს მოითხოვს და დიდი მიმდევრობებისთვის პრაქტიკულად ვერ მივიღებთ პასუხს.
თუ დავაკვირდებით მიმდევრობებს, გამოჩნდება, რომ დიდი ამოცანა შეგვიძლია დავყოთ ქვეამოცანებად, სადაც ქვეამოცანა შეესაბამება მოცემული მიმდევრობების პრეფიქსთა წყვილებისთვის უდიდესი საერთო ქვემიმდევრობის პოვნას.
ინტუიციურია, მაგრამ მაინც განვსაზღვროთ მიმდევრობის ”პრეფიქსის” ცნება. თუ მოცემული გვაქვს მიმდევრობა X = (x1, x2, … , xm), მისი i-ური პრეფიქსი იქნება X-ის პირველი i ცალი ელემენტისგან შემდგარი მიმდევრობა, ანუ Xi = (x1, x2, … , xi). რა თქმა უნდა i4 = (A,B,C,B). X0 ცარიელი მიმდევრობაა.
სანამ ამოცანის ამოხსნაზე გადავალთ ერთი პატარა თეორემა უნდა დავამტკიცოთ.
თეორემა:
მოცემულია X = (x1, x2, … , xm) და Y = (y1, y2, … , yn) მიმდევრობები. ხოლო Z = (z1, z2, … , zk) არის ამ მიმდევრობების უდიდესი საერთო ქვემიმდევრობა.
1. თუ xm = yn, მაშინ zk = xm = yn და Zk-1 არის Xm-1 და Yn-1 პრეფიქსების უსქ (უდიდესი საერთო ქვემიმდევრობა).
2. თუ xm !=yn, მაშინ zk != xm-დან გამომდინარეობს, რომ Z არის Xm-1 და Yn პრეფიქსების უსქ.
3. თუ xm !=yn მაშინ, zk != yn-დან გამომდინარეობს, რომ Z არის Xm და Yn-1 პრეფიქსების უსქ.
დამტკიცება საკმაოდ მარტივია.
1. დავუშვათ საწინააღმდეგო და ვთქვათ, რომ zk != xm. რადგან xm = yn, Z-ს შეგვიძლია მივამატოთ xm ელემენტიც. ამ შემთხვევაში კი გამოვა რომ უდიდესი საერთო ქვემიმდევრობა Z-ზე გრძელია და წინააღმდეგობას მივიღებთ. მოკლედ რომ ვთქვათ, თუ მოცემული მიმდევრობების ბოლო ელემენტები ერთნაირია, ის ელემენტი აუცილებლად იქნება უსქ-ის ბოლო ელემენტი.
დებულების მეორე ნაწილიც იგივე პრინციპით დავამტკიცოთ. ვთქვათ Zk-1 არ არის Xm-1 და Yn-1 პრეფიქსების უსქ. მაშინ იარსებებს რაიმე უსქ W, რომლის სიგრძეც k-1-ზე მეტია. მას რომ მივამატებთ xm = yn ელემენტს, ის k-ს გადააჭარბებს. ეს წინააღმდეგობაა.
2. რომ არსებობდეს Xm-1 და Y-ის უდიდესი საერთო ქვემიმდევრობა – W, რომლის ელემენტების რაოდენობა k-ზე მეტია, ის აგრეთვე იქნებოდა X-ის და Y-ის უსქ და თან Z-ს გადააჭარბებდა სიგრძეში. მოცემულობის მიხედვით კი Z არის X-ის და Y-ის უსქ.
3. მეორე პუნქტის ანალოგიურად მტკიცდება.
ამ თეორემიდან კარგად ჩანს რომ ორი მიმდევრობის უდიდესი საერთო ქვემიმდევრობა თავის თავში შეიცავს ამ მიმდევრობების პრეფიქსების უდიდეს საერთო ქვემიმდევრობას და მის საპოვნელად რეკურენტული ფორმულა შეგვიძლია შევადგინოთ.
თუმცა ცხადია, რომ პირდაპირი რეკურსია სრულ გადარჩევას გააკეთებს, რადგან მისი განშტოებები ძალიან ხშირად ერთსა და იმავე ქვეამოცანას ამოხსნიან. ამიტომ, როდესაც დავადგენთ უდიდეს ქვემიმდევრობის სიგრძეს თითოეული პრეფიქსისთვის, დავიმახსოვროთ ის და მეორედ აღარ მოვძებნოთ იგივე პრეფიქსის უსქ.
კონკრეტულად, შემოვიღოთ რიცხვითი ტიპის ორგანზომილებიანი მასივი c და მის [i][j] უჯრაში შევინახოთ Xi და Yj პრეფიქსების უსქ-ის სიგრძე.
როცა i ან j ნოლის ტოლია მაშინ c[i][j]-ის მნიშვნელობა ნოლის ტოლი იქნება რადგან საერთო ქვემიმდევრობაც ცარიელი გამოვა პრეფიქსის მსგავსად.
როცა i, j >0 და xi = yj, ეს ნიშნავს რომ Xi და Yi მიმდევრობების უსქ-ის სიგრძე ერთით მეტია ვიდრე Xi-1 და Yi-1 მიმდევრობების უსქ-ის სიგრძე, რადგან ერთი კიდევ ერთი საერთო ელემენტი დაემატა.
როცა i,j>0 და xi != yj, ეს ნიშნავს რომ უსქ-ის სიგრძე იგივეა რაც Xi-1 და Yj პრეფიქსების ან Xi და Yj-1 პრეფიქსების უსქ-ს ჰქონდა. ამიტომ ამ ორიდამ მაქსიმალური სიგრძისა ავირჩიოთ და მისი მნიშვნელობით შევავსოთ c[i][j] უჯრა.
საბოლოოდ ასეთი რეკურენტული ფორმულა მივიღეთ:
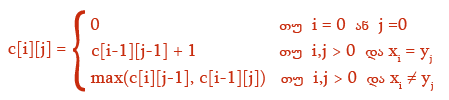
თუმცა საბოლოო პასუხი არა მხოლოდ უდიდესი საერთო ქვემიმდევრობის სიგრძეა, არამედ თვითონ ქვემიმდევრობა. ამიტომ შემოვიღოთ c-ის ზომის კიდევ ერთი დამატებითი ორგანზომილებიანი მასივი b, რომლის [i][j] უჯრაში შევინახავთ ხოლმე თუ რომელი მეთოდით შევავსეთ c[i][j].
ფსევდო კოდი ასე გამოიყურება:
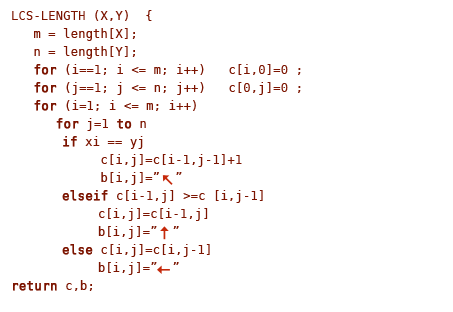
კოდში კარგად ჩანს რომ ორი ჩადგმული ციკლი მუშაობს. მათგან ერთი m, ხოლო მეორე n ცალ იტერაციას აკეთებს. თითო უჯრის მნიშვნელობის გამოთვლა O(1) დროში ხდება. ანუ ალგორითმი O(mn) დროში მუშაობს, სადაც m და n მოცემული მიმდევრობების სიგრძეებია.
ვნახოთ როგორ შეავსებს ეს ფუნქცია მასივებს ჩვენს მაგალითზე დაყრდნობით:
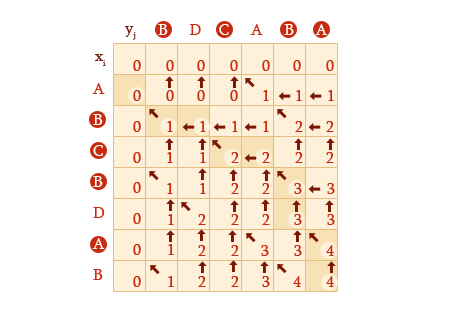
მხოლოდ ისღა დაგვრჩენია რომ ამ მონაცემებიდან უდიდესი საერთო ქვემიმდევრობა აღვადგინოთ. ამისთვის პატარა რეკურსიული ფუნქცია გამოვიყენოთ.
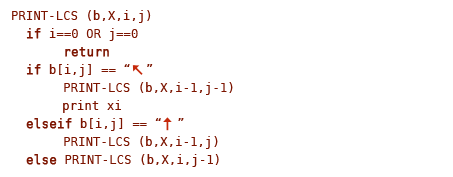
ეს ფუნქცია O(m + n) დროში მუშაობს, რადგან ის ყოველ ჯერზე მინიმუმ ან i-ის ამცირებს ერთით, ან j-ის, ან საერთოდ ორივეს ერთად.
შევაფასოთ გამოყენებული მეხსიერებაც. ამ ალგორითმში ორი ცალი m x n ზომის მასივი გვაქვს, ამიტომ O(mn) მეხსიერებას ვიყენებთ. შეიძლება b მასივი საერთოდ გამოვტოვოთ, თუმცა მეხსიერების O(mn) შეფასება არ შეიცვლება.
საქმე იმაშია, რომ c[i][j] უჯრის მეზობელ c[i-1][j-i], c[i][j-1], c[i-1][j] უჯრებს თუ დავათვალიერებთ, მარტივად მივხვდებით რომელ მათგანზე დაყრნობით მივიღეთ c[i][j] მნიშვნელობა და აღარ დაგვჭირდება ამის b მასივში შენახვა.
განახლება კომენტარიდან:
Zuba Dalama:
ერთ-ერთი “real world” მაგალითია diff: http://en.wikipedia.org/wiki/Diff
ვისაც აინტერესებს თუ როგორაა რეალიზებული იხ. google–ის opensource პროექტი (წარმოდგენილია შემდეგ ენებზე: Java, JavaScript, Dart, C++, C#, Objective C, Lua და Python) http://code.google.com/p/google-diff-match-patch/
და მისი დოკუმენტაცია: http://neil.fraser.name/writing/diff/.